Tic-tac-toe

Tic-tac-toe

Game play of Tic-tac-toe
Genre(s)	Paper and pencil game
Players	2
Setup time	Minimal
Playing time	~1 min
Random chance	None
Skill(s) required	Strategy

Tic-tac-toe, also called noughts and crosses (in the UK, Australia, New Zealand, South Africa, India and the rest of the British Commonwealth countries), is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first. The player who succeeds in placing three respective marks in a horizontal, vertical, or diagonal row wins the game.

The following example game is won by the first player, X:

Players soon discover that best play from both parties leads to a draw (often referred to as cat or cat's game). Hence, tic-tac-toe is most often played by young children.

The friendliness of tic-tac-toe games makes them ideal as a pedagogical tool for teaching the concepts of good sportsmanship and the branch of artificial intelligence that deals with the searching of game trees. It is straightforward to write a computer program to play tic-tac-toe perfectly, to enumerate the 765 essentially different positions (the state space complexity), or the 26,830 possible games up to rotations and reflections (the game tree complexity) on this space.

Contents 1 History 2 Combinatorics 2.1 Number of terminal positions 2.2 Number of possible games 3 Strategy 4 Variations 5 Alternative English names 6 In popular culture 7 See also 8 References 9 External links

History

An early variant of Tic-tac-toe was played in Roman Empire, around the first century BC. It was called Terni Lapilli and instead of having any number of pieces, each player only had three, thus they had to move them around to empty spaces to keep playing. The game's grid markings have been found chalked all over Rome.

However, according to Claudia Zaslavsky's book Tic Tac Toe: And Other Three-In-A Row Games from Ancient Egypt to the Modern Computer, Tic-Tac-Toe could originate back to ancient Egypt.^[1]

The different names of the game are more recent. The first print reference to "noughts and crosses", the British name, appeared in 1864. The first print reference to a game called "tick-tack-toe" occurred in 1884, but referred to "a children's game played on a slate, consisting in trying with the eyes shut to bring the pencil down on one of the numbers of a set, the number hit being scored". "Tic-tac-toe" may also derive from "tick-tack", the name of an old version of backgammon first described in 1558. The U.S. renaming of noughts and crosses as tic-tac-toe occurred in the 20th century.^[2]

In 1952, Tic-tac-toe became the first known video game, OXO (or Noughts and Crosses) for the EDSAC computer. The computer player could play perfect games of tic-tac-toe against a human opponent.

In 1975, Tic-Tac-Toe was also used by MIT students to demonstrate the computational power of Tinkertoy elements. The Tinkertoy computer, made out of (almost) only Tinkertoys, is able to play Tic-Tac-Toe perfectly^[3]. It is currently on display at the Museum of Science, Boston.

Combinatorics

Despite its apparent simplicity, Tic-tac-toe requires detailed analysis to determine even some elementary combinatory facts, the most interesting of which are the number of possible games and the number of possible positions. A position is merely a state of the board, while a game usually refers to the way a terminal position is obtained.

A naive count of the number of positions leads to 19,683 possible board layouts (3⁹ since each of the nine spaces can be X, O or blank), and a similar count of the number of games leads to 362,880 (i.e. 9!) different sequences for placing the Xs and Os on the board. However, this doesn't take into account the fact that the game ends when three-in-a-row is obtained. Many of the 19,683 positions are unreachable in an actual game.

The complete analysis is further complicated by the definitions used when setting the conditions, like board symmetries.

Number of terminal positions

When considering only the state of the board, and after taking into account board symmetries (i.e. rotations and reflections), there are only 138 terminal board positions. Assuming that X makes the first move every time:

• 91 unique positions are won by (X)
• 44 unique positions are won by (O)
• 3 unique positions are drawn

Number of possible games

Without taking symmetries into account, the number of possible games can be determined by hand with an exact formula that leads to 255,168 possible games (see Henry Bottomley, 2001^[4], or Steve Schaeffer, 2002^[5]). Assuming that X makes the first move every time:

• 131,184 finished games are won by (X)
• 77,904 finished games are won by (O)
• 46,080 finished games are drawn

If board symmetries are taken into account, two games are considered the same if the sequence of board modulo the symmetries is the same. With the use of computer, Steve Schaeffer determined in 2002^[5] that the number of games in these conditions is 26,830.

Strategy

A player can play perfect tic-tac-toe (win or draw) given they move according to the highest possible move from the following table.^[7]

1. Win: If the player has two in a row, play the third to get three in a row.
2. Block: If the [opponent] has two in a row, play the third to block them.
3. Fork: Create an opportunity where you can win in two ways.
4. Block opponent's Fork:
   • Option 1: Create two in a row to force the opponent into defending, as long as it doesn't result in them creating a fork or winning. For example, if "X" has a corner, "O" has the center, and "X" has the opposite corner as well, "O" must not play a corner in order to win. (Playing a corner in this scenario creates a fork for "X" to win.)
   • Option 2: If there is a configuration where the opponent can fork, block that fork.
5. Center: Play the center.
6. Opposite corner: If the opponent is in the corner, play the opposite corner.
7. Empty corner: Play in a corner square.
8. Empty side: Play in a middle square on any of the 4 sides.

The first player, whom we shall designate "X", has 3 possible positions to mark during the first turn. Superficially, it might seem that there are 9 possible positions, corresponding to the 9 squares in the grid. However, by rotating the board, we will find that in the first turn, every corner mark is strategically equivalent to every other corner mark. The same is true of every edge mark. For strategy purposes, there are therefore only three possible first marks: corner, edge, or center. Player X can win or force a draw from any of these starting marks; however, playing the corner gives the opponent the smallest choice of squares which must be played to avoid losing.^[8]

The second player, whom we shall designate "O", must respond to X's opening mark in such a way as to avoid the forced win. Player O must always respond to a corner opening with a center mark, and to a center opening with a corner mark. An edge opening must be answered either with a center mark, a corner mark next to the X, or an edge mark opposite the X. Any other responses will allow X to force the win. Once the opening is completed, O's task is to follow the above list of priorities in order to force the draw, or else to gain a win if X makes a weak play.

To guarantee a tie if you're O though, if X doesn't play center (playing a corner is the best opening move), take center, and then a side middle. This will stop any forks from happening. If you play a corner, a perfect X player has already played the corner opposite his first and proceeds to play a 3rd corner, stopping your 3-in-a-row and making his own fork. If X plays center opening move, just keep your eyes open and he won't be able to fork you. If you are X, play a corner first. If O takes center (best move for him), take the corner oppsotie your original, and proceed as detailed above. If O plays a corner or side-middle first, you are guaranteed to win. If corner, simply take any of the other 2 corners, and then the last. You've forked him. If he plays a side-middle, take the only corner that his blocking won't make 2 in a row. he'll block, but the best of the other two, you'll see which one, and you'll fork him. The only way for X not to win is for O to play middle and then a side-middle.

Variations

Many board games share the element of trying to be the first to get n-in-a-row: three men's morris, nine men's morris, pente, gomoku, Qubic, Connect Four, Quarto, Gobblet. Generalizing the original Tic-tac-toe game, we get the 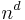-game, played on the -dimensional cube with edge .^[9] Then, the ordinary Tic-tac-toe is the 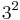-game. The m,n,k-games are a family of generalized games based on tic-tac-toe.

• 3-dimensional tic-tac-toe on a 3×3×3 board, though the first player has an easy win by playing in the centre if 2 people are playing. Another variant is played on a 4×4×4 board, though it was solved by Oren Patashnik in 1980 (the first player can force a win).^[10] A more complex variant can be played on boards utilising higher dimensional space, most commonly 4 dimensions in a 3×3×3×3 board. In such games the aim is to fill up the board and get more rows of three in total than the other player or to play with 4 people and get 1 row of 3.
• In misère tic-tac-toe the player wins if the opponent gets n in a row. A 3×3 game is a draw.
• Tic Tac Tactic: A new game played on a three-dimensional board. Each player takes it in turns to send their ball at least half way round the curved board until it drops down into one of the 9 indents of the 3 x 3 grid. The player wins balls by forming a row of 3, and they can, using a rubber device, change the outcome of their ball's path and bounce their ball to where they want. Each 3-in-a-row wins a ball of the player. The winner is skilful enough to have won five balls off his opponent.
• In nine board tic-tac-toe nine tic-tac-toe boards are themselves arranged in a 3×3 grid. The first player's move may go on any board; all moves afterwards are placed in the empty spaces on the board corresponding to the square of the previous move (that is, if a move were in the upper-left square of a board, the next move would take place on the upper-left board). If a player cannot move because the indicated board is full, the next move may go on any board. Victory is attained by getting 3 in a row on any board. This makes the game considerably longer and more involved than tic-tac-toe, with a definite opening, middle game and endgame.
• super tic-tac-toe is played like nine board tic-tac-toe except that the game does not end when a player wins a game on one of the small boards. Instead, the position of the small board where that player won is marked on a 3x3 grid, and a player wins when they form 3-in-a-row on that grid.
• In Tic-Tac-Chess, players play a game of chess and tic-tac-toe simultaneously. When a player captures an opponent's piece, the player can make a play on the tic-tac-toe board regardless if the other player has not yet made a play. The first person to get 3 X's or O's in a row wins the game. This makes for a much more defensive game of chess.
• There is a game that is isomorphic to tic-tac-toe, but on the surface appears completely different. Two players in turn say a number between one and nine. A particular number may not be repeated. The game is won by the player who has said three numbers whose sum is 15. Plotting these numbers on a 3×3 magic square shows that the game exactly corresponds with tic-tac-toe, since three numbers will be arranged in a straight line if and only if they total 15. This can be helpful in programming computer adaptations of the game, by assigning the squares of the grid to their corresponding number on the magic square.
• Two players fill out a 3×3 grid with numbers one through nine in order of priority. They then compare their grids and play tic-tac-toe by filling in the squares by the priority they listed before.
• In the 1970s, there was a two player game made by Tri-ang Toys & Games called Check Lines, in which the board consisted of eleven holes arranged in a geometrical pattern of twelve straight lines each containing three of the holes. Each player had exactly five tokens and played in turn placing one token in any of the holes. The winner was the first player whose tokens were arranged in two lines of three (which by definition were intersecting lines). If neither player had won by the tenth turn, subsequent turns consisted of moving one of one's own tokens to the remaining empty hole, with the constraint that this move could only be from an adjacent hole.
• Toss Across is a tic-tac-toe game where players throw bean bags at a large board to mark squares.
• Star Tic Tac Toe is tic-tac-toe game where it is played with checkers like movable pieces on 3×3 board. Each player gets 3 pieces.The players move the pieces into empty cells until someone wins. This adds dynamism. In addition each player gets a special piece marked with a star. The stars can be swapped. This adds surprise.
• Mojo, Mojo Too and Mojo 2 is a tic-tac-toe game played on a 3×3 board with original and unique movable pieces and pawns - the latter is played for points. The players move the pieces and pawn(s) onto empty positions until someone wins.
• The object of the fictional D'ni game of Gemedet is to get six balls in-a-row in a 9×9×9 cube grid.
• The object of the fictional game Squid-Tac-Toad is to get four (or five) pieces in-a-row on a 4×4 or 5×5 checkerboard grid.
• Some children play where getting a Y formation also counts as a win. This effectively guarantees a win, since all of the game scenarios feature some form of Y formation.
• Quantum tic tac toe allows players to place a quantum superposition of numbers on the board, i.e. the players' moves are "superpositions" of plays in the original classical game. This variation was invented by Allan Goff of Novatia Labs.^[11]
• Another variation on tic-tac-toe is played on a larger grid (say 10x10) where the object is to get 5 in a row. The increased amount of space creates a greater complexity.
• There is a variation on tic-tac-toe that is popular in Vietnam, in which the player has to get 5 in a row to win the game. Each player takes turns to mark "x" or "o" on the board. The strategy is to not only block the opponent, but create chances for yourself to form 5 in a row in any direction. The board is unlimited and has no boundary until one wins. See Go-moku
• The game can also be varied by limiting the number of pieces and then allowing movement. The three-a-side then becomes Three Men's Morris (see Nine Men's Morris).
• There is a variation using a list of the words eat, an, laf, it, line, if, lot, on and foe. To win, a player must select three words with the same letter. If the words are plotted on a tic-tac-toe grid in order a three in a row line wins.
• Memory tic-tac-toe is played with the same rules as standard tic-tac-toe. However, instead of marking moves on a piece of paper, the games is played verbally, with each player calling out which locations they take. The most used naming convention is referring to the locations as points as their corresponding cardinal and ordinal points with ″center" referring to the middle piece. In addition to the standard win condition, an optional lose condition may be implemented for a player that "re-touches" an already occupied square. Due to both players trying to keep all the board positions in memory, it may be useful for a third person keep track of the game on paper out of view of the players.

Alternative English names

The game has a number of alternative English names.

• Tick-tack-toe, tic-tac-toe, tick-tat-toe, or tit-tat-toe (USA, Canada)
• Noughts and crosses or Naughts and crosses (Great Britain, Republic of Ireland, Australia, New Zealand, South Africa)
• Exy-Ozys, Xsie-Osies (verbal name only) (Northern Ireland)
• Xs and Os (Egypt, Republic of Ireland, Canada, Scotland, Zimbabwe, India)
• O-X (Mauritius)

In the United States, the name "noughts and crosses" is not well understood, as the word "nought" is archaic in usage and X-shaped objects are not generally called crosses except in the case of specific named crosses like St. Patrick's Cross.

Sometimes, the games Tic-tac-toe (where players keep adding "pieces") and Three Men's Morris (where pieces start to move after a certain number have been placed) are confused with each other.

In popular culture

In the 1983 film WarGames, tic-tac-toe is used as an allegory for nuclear war. In the climax of the film, the protagonist prevents an out of control military defense computer from launching nuclear missiles by making it repeatedly play tic-tac-toe against itself. After quickly learning that good strategy by both players produces no winner, the computer then plays through all known nuclear strike scenarios, again finding no winner. The computer concludes, "Strange game. The only winning move is not to play."

Various game shows have been based on Tic-Tac-Toe and its variants:

• On Hollywood Squares, nine celebrities filled the cells of the tic-tac-toe grid; players put symbols on the board by correctly agreeing or disagreeing with a statement the celebrity makes.
• In Tic-Tac-Dough, players put symbols up on the board by answering questions in various categories.
• In Beat the Teacher, contestants answer questions to win a turn to influence a tic-tac-toe grid.
• On The Price Is Right, several national variants feature a pricing game called "Secret X," in which players must guess prices to win Xs to place on a blank board. They must place the Xs in position to guess the location of the titular "secret X" hidden in the center column of the board and form a tic-tac-toe line across. There are no Os in this variant of the game.
• On Minute to Win It, the game Ping Tac Toe has one contestant playing the game with nine water-filled glasses and white and orange ping-pong balls, trying to get three in a row of either color. They must alternate colors after each successful landing and must be careful not to block themselves.

See also

• 3-D Tic-Tac-Toe
• SOS (game)

References

External links

• Wolfram's MathWorld